Basic logic symbols

Symbol	Name	Explanation	Examples	Unicode Value	HTML Entity	LaTeX symbol
	Read as
	Category
⇒ → ⊃	material implication	A ⇒ B is true only in the case that either A is false or B is true. → may mean the same as ⇒ (the symbol may also indicate the domain and codomain of a function; see table of mathematical symbols). ⊃ may mean the same as ⇒ (the symbol may also mean superset).	x = 2 ⇒ x² = 4 is true, but x² = 4 ⇒ x = 2 is in general false (since x could be −2).	U+21D2 U+2192 U+2283	⇒ & rarr; & sup;	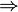$\Rightarrow$ \Rightarrow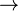 $\to$ \to $\supset$ \supset $\implies$ \implies
	implies; if .. then
	propositional logic, Heyting algebra
⇔ ≡ ↔	material equivalence	A ⇔ B is true only if both A and B are false, or both A and B are true.	x + 5 = y + 2 ⇔ x + 3 = y	U+21D4 U+2261 U+2194	⇔ & equiv; & harr;	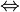$\Leftrightarrow$ \Leftrightarrow $\equiv$ \equiv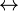 $\leftrightarrow$ \leftrightarrow $\iff$ \iff
	if and only if; iff; means the same as
	propositional logic
¬ ˜ !	negation	The statement ¬A is true if and only if A is false. A slash placed through another operator is the same as "¬" placed in front.	¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y)	U+00AC U+02DC	¬ & tilde; ~	$\neg$ \lnot or \neg $\sim$ \sim
	not
	propositional logic
∧ • &	logical conjunction	The statement A ∧ B is true if A and B are both true; else it is false.	n < 4 ∧ n >2 ⇔ n = 3 when n is a natural number.	U+2227 U+0026	∧ & amp;	$\wedge$ \wedge or \land \&^[1]
	and
	propositional logic, Boolean algebra
∨ + ǀǀ	logical (inclusive) disjunction	The statement A ∨ B is true if A or B (or both) are true; if both are false, the statement is false.	n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 when n is a natural number.	U+2228	∨	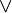$\lor$ \lor or \vee
	or
	propositional logic, Boolean algebra
⊕ ⊻	exclusive disjunction	The statement A ⊕ B is true when either A or B, but not both, are true. A ⊻ B means the same.	(¬A) ⊕ A is always true, A ⊕ A is always false.	U+2295 U+22BB	⊕	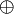$\oplus$ \oplus $\veebar$ \veebar
	xor
	propositional logic, Boolean algebra
⊤ T 1	Tautology	The statement ⊤ is unconditionally true.	A ⇒ ⊤ is always true.	U+22A4	T	$\top$ \top
	top, verum
	propositional logic, Boolean algebra
⊥ F 0	Contradiction	The statement ⊥ is unconditionally false.	⊥ ⇒ A is always true.	U+22A5	⊥ F	$\bot$ \bot
	bottom, falsum, falsity
	propositional logic, Boolean algebra
∀ ()	universal quantification	∀ x: P(x) or (x) P(x) means P(x) is true for all x.	∀ n ∈ ℕ: n² ≥ n.	U+2200	∀	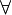$\forall$ \forall
	for all; for any; for each
	first-order logic
∃	existential quantification	∃ x: P(x) means there is at least one x such that P(x) is true.	∃ n ∈ ℕ: n is even.	U+2203	∃	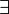$\exists$ \exists
	there exists
	first-order logic
∃!	uniqueness quantification	∃! x: P(x) means there is exactly one x such that P(x) is true.	∃! n ∈ ℕ: n + 5 = 2n.	U+2203 U+0021	∃ !	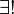$\exists !$ \exists !
	there exists exactly one
	first-order logic
:= ≡ :⇔	definition	x := y or x ≡ y means x is defined to be another name for y (but note that ≡ can also mean other things, such as congruence). P :⇔ Q means P is defined to be logically equivalent to Q.	cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B)	U+2254 (U+003A U+003D) U+2261 U+003A U+229C	:= : & equiv; & hArr;	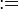$:=$ := $\equiv$ \equiv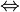 $\Leftrightarrow$ \Leftrightarrow
	is defined as
	everywhere
( )	precedence grouping	Perform the operations inside the parentheses first.	(8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, but 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4.	U+0028 U+0029	( )	$(~)$ ( )
	parentheses, brackets
	everywhere
⊢	Turnstile	x ⊢ y means y is provable from x (in some specified formal system).	A → B ⊢ ¬B → ¬A	U+22A2	⊢	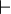$\vdash$ \vdash
	provable
	propositional logic, first-order logic
⊨	double turnstile	x ⊨ y means x semantically entails y	A → B ⊨ ¬B → ¬A	U+22A8	⊨	$\vDash$ \vDash
	entails
	propositional logic, first-order logic